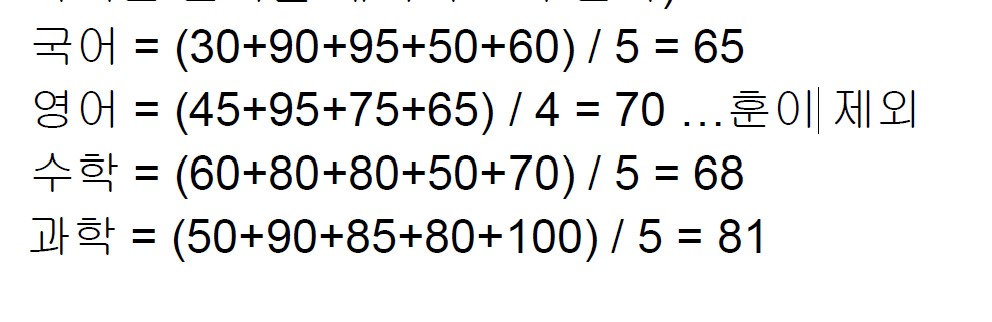게임학원 사전캠프 레벨테스트

개강 전 사전캠프 레벨테스트

게시 2025/03/09 업데이트 2025/03/10

By Jinyeong LEE

12 분읽는 시간

게임학원 사전캠프 레벨테스트

게임학원 개강 전 레벨테스트를 진행했다.
학생들의 수준을 파악하고 수업 내용의 난이도를 조절하기 위함이 아닌가 생각된다
복습 차원에서 다시 풀어보고 정리하고자 한다.

문제1

1차 방정식 문제였다.

문제2

\(3\times2\times1 = 6\)
경우의 수 문제

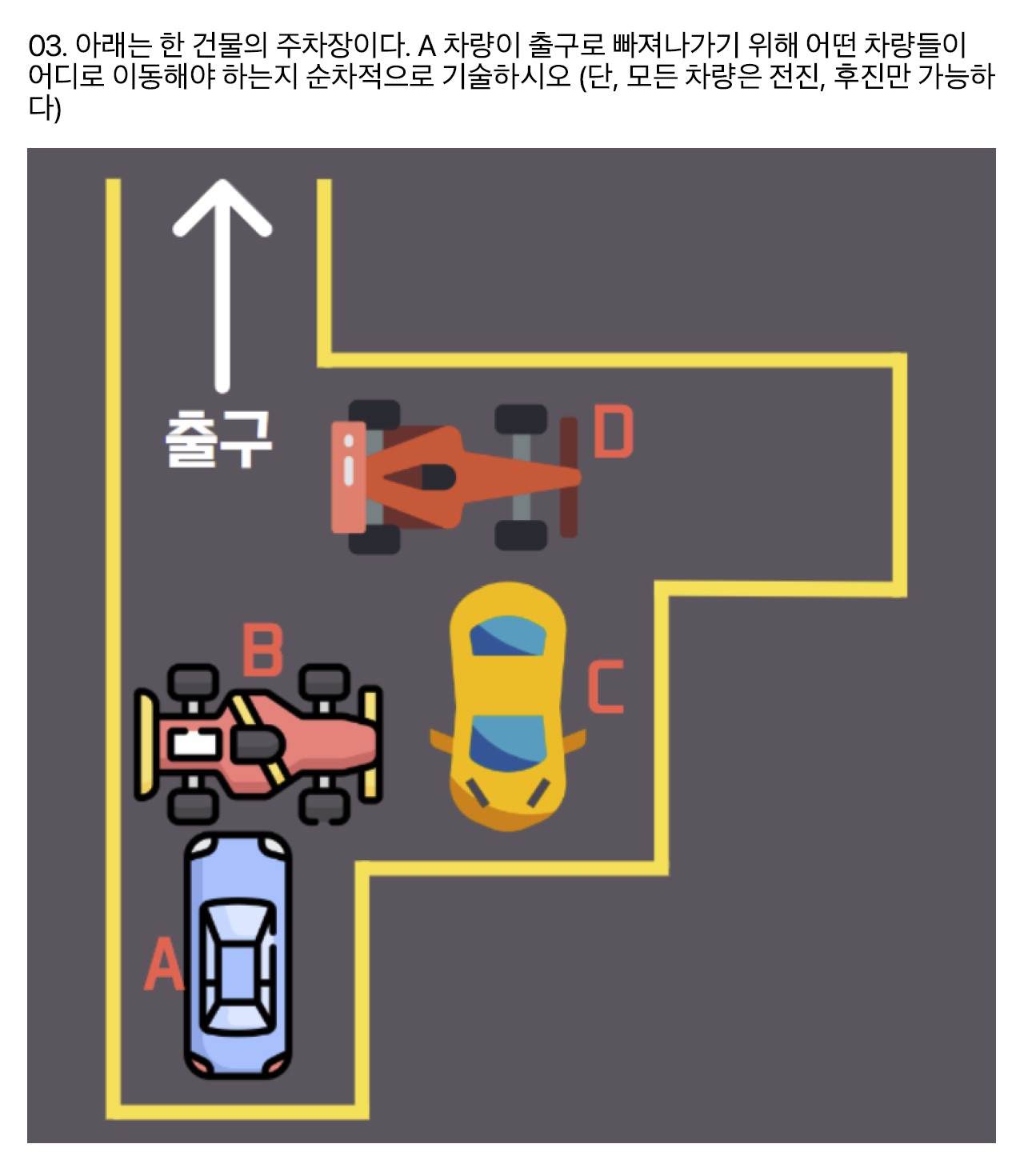
문제3

D 전진 -> C 후진 -> B 전진 -> A 전진

문제4

856394127
코딩은 순서를 틀리면 안된다는 교훈을 준다.

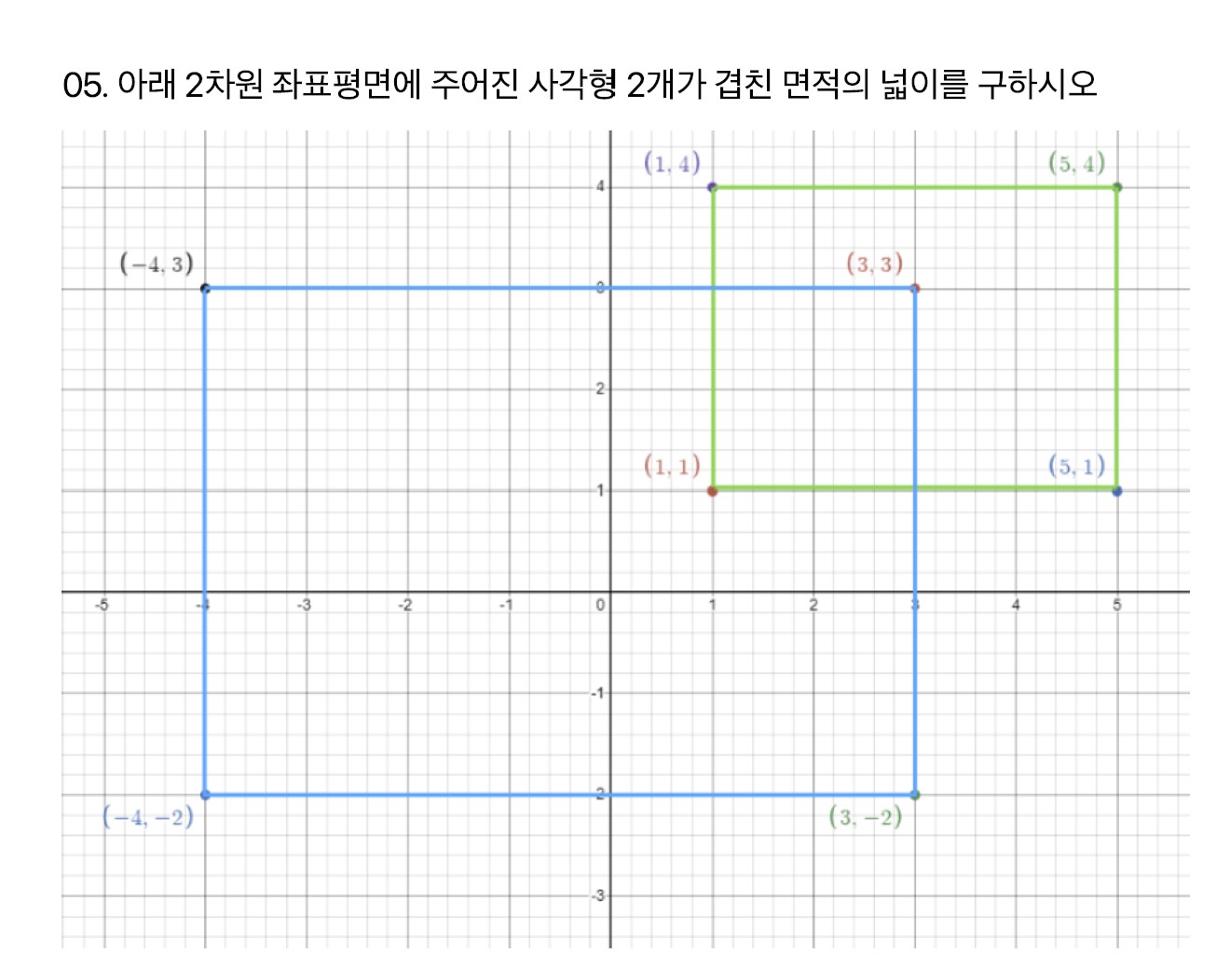
문제5

겹친 부분의 밑변 = A
겹친 부분의 높이 = B
겹친 부분의 넓이 = A X B
\(A=3-1 =2\)
\(B=3-1=2\)
\(A \times B = 4\)

문제6

\(7^3=343\)
\(\frac{(343\times5)+(2\times19)-8}{5} = 349\)

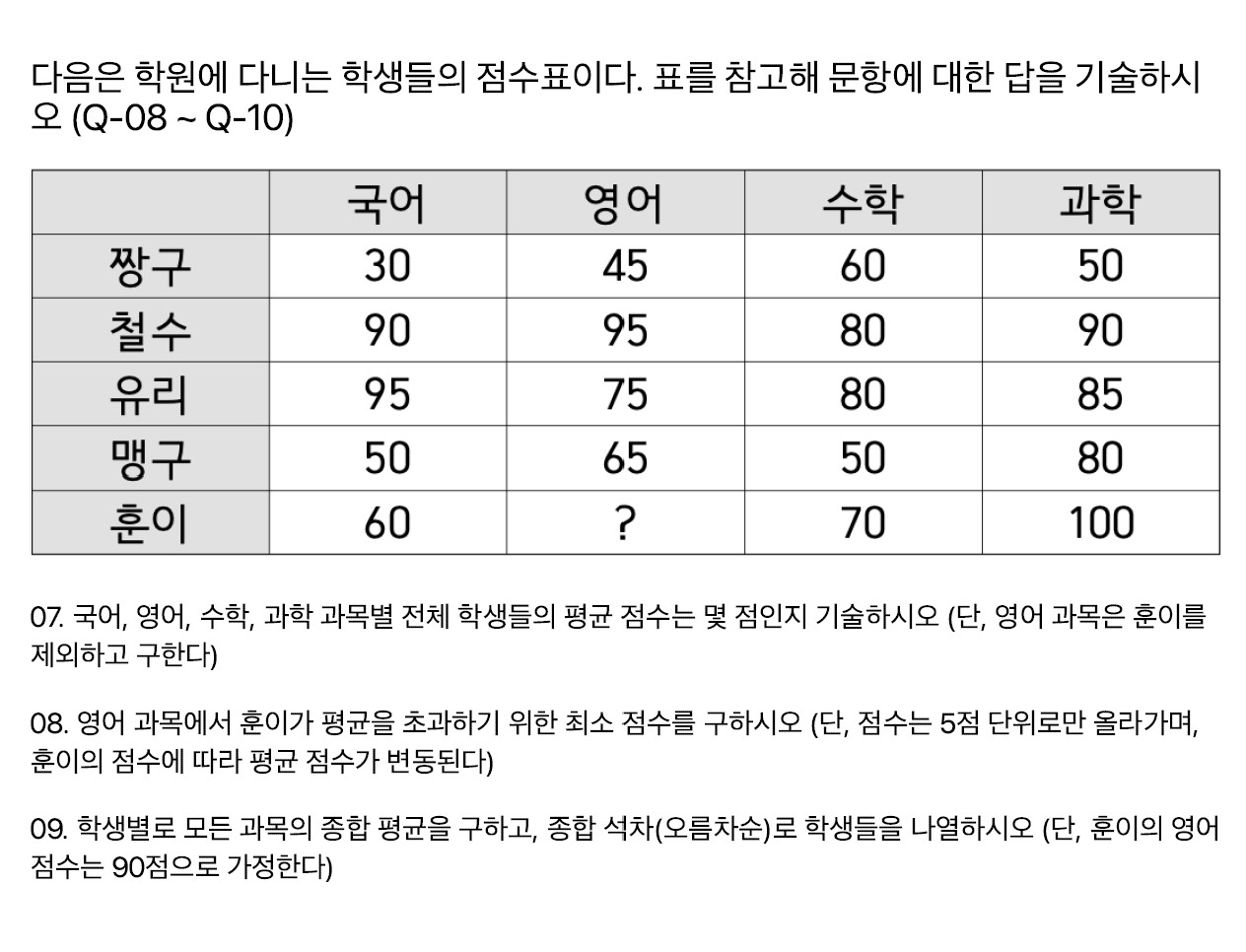
문제7~9

7번 문제의 정답

8번 문제의 정답

9번 문제의 정답
이 문제들은 아마 후에 배열을 다룰 때 나올 것 같다.

문제10

두 구의 반지름을 더한 값과 같거나 그보다 작으면 충돌했다고 할 수 있다.

\(14+17=31\)
그러므로 31보다 작거나 같으면 충돌했다고 할 수 있다.

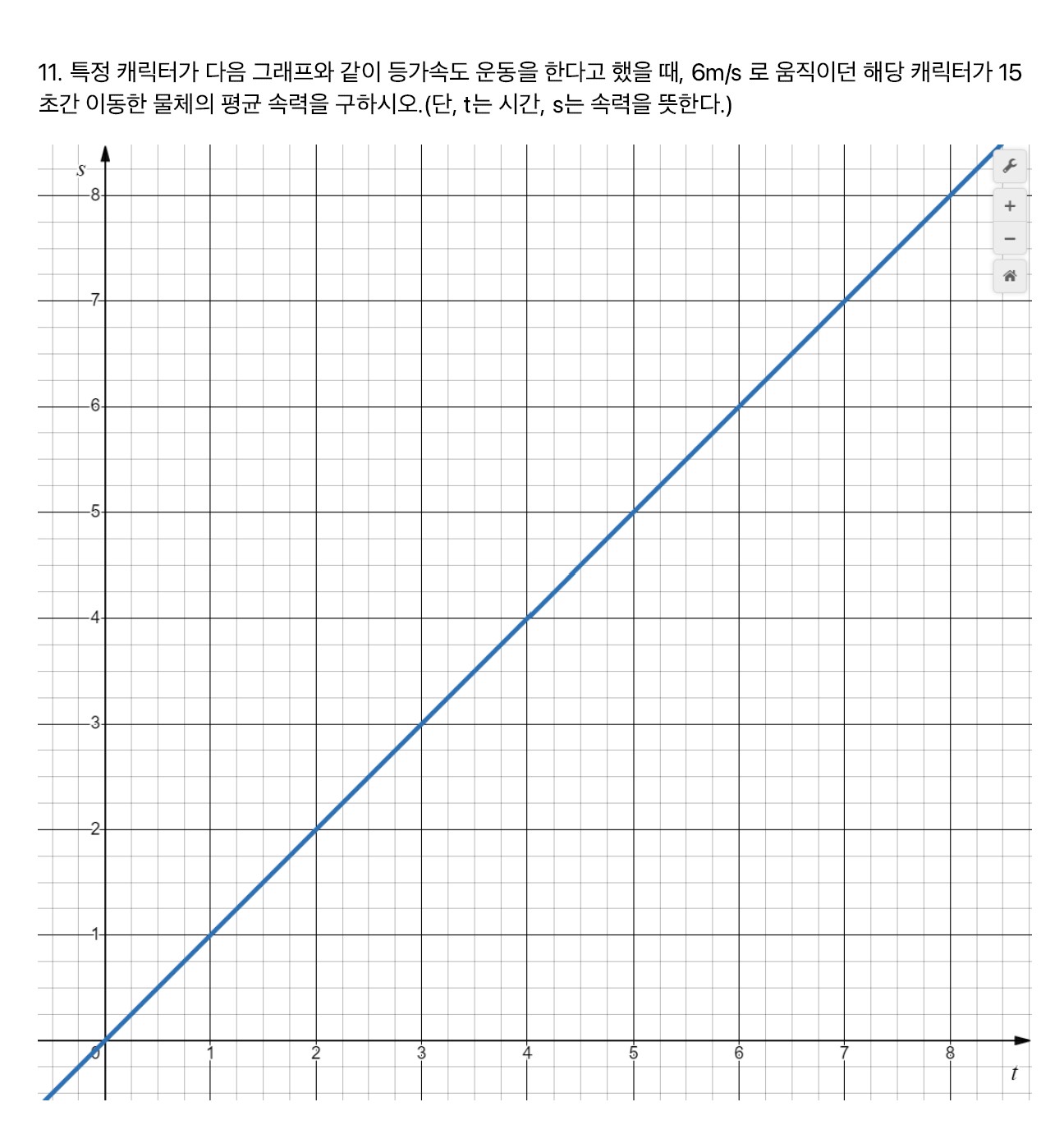
문제11

해당 문제는 두 가지 방향으로 풀어질 수 있다.

그래프에서 기울기 정보만 취사선택 하여 문제를 푸는 방법
그래프만 보고 푸는 방법

가속도가 1, 초기속도가 0m/s 일 경우
- 초기 속도가 0m/s, 가속도가 1m/s^2 인 경우이므로, 간단하게 그래프 상에서 넓이만 구하면 된다.
  t= 15일때, s도 15 이므로 총 이동거리는 다음과 같다.
- \[\frac{15\times15}{2} = 225\div2\]
- 평균속력은 총 이동거리에 다시 시간으로 나눠주면 된다
- \[225\div15=7.5(m/s)\]
가속도가 1, 초기속도가 6m/s 일 경우
- 총 이동거리는 1번 에서의 값과 초기속도 6m/s의 15초동안의 거리만 구해서 더하면 된다.
- \[112.5+90=202.5\]
- 평균 속력은 같은 방식으로 구한다
- \[202.5\div15=13.5(m/s)\]

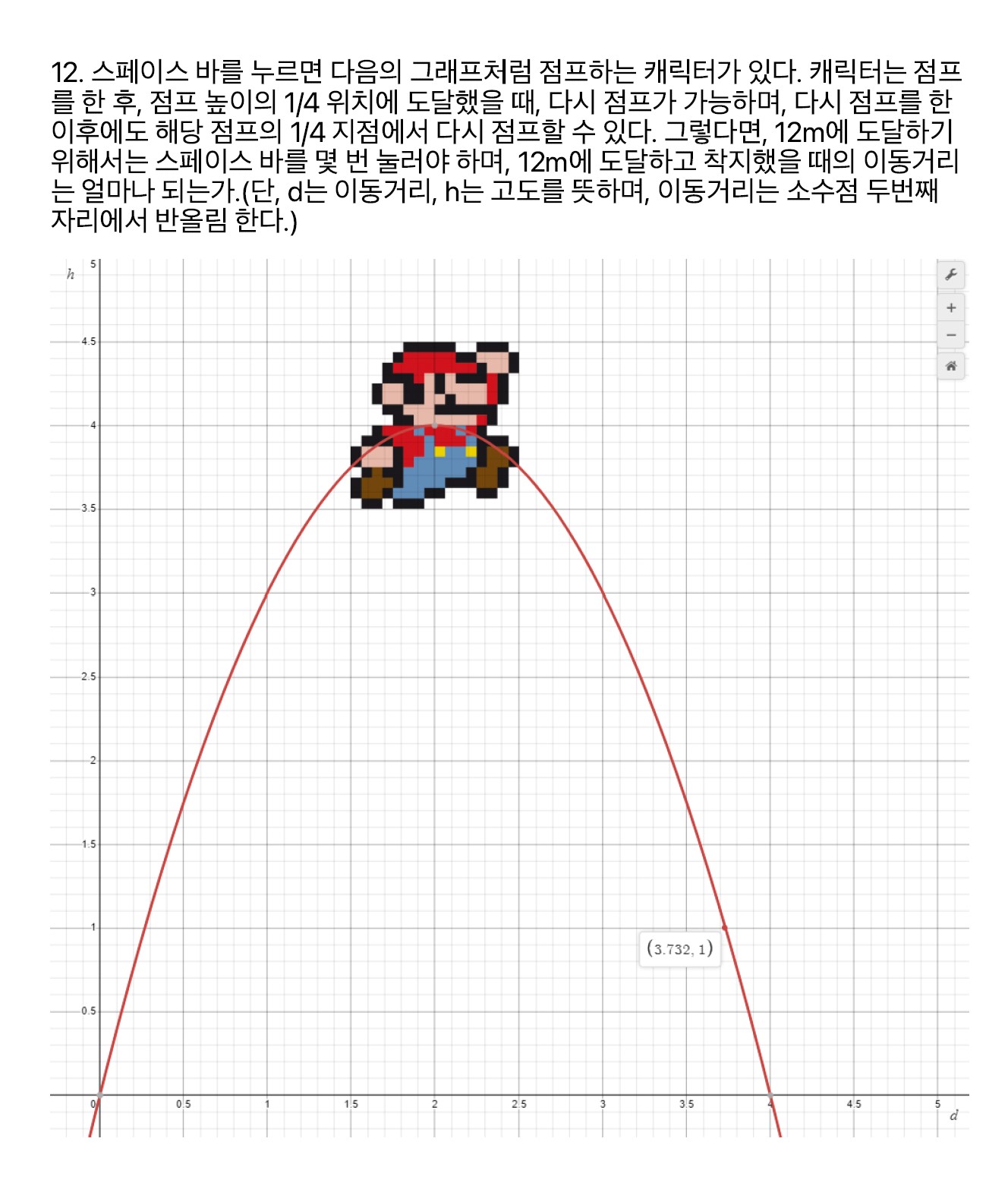
문제12

생각보다 함정인 문제였다. 쉬워보이지만 전혀 그렇지 않다.
점프 횟수는 동일하게 9번이 맞는데, 이동거리가 함정이다.
12미터 위에서 땅까지 착지 했을 때의 거리를 알아야 해서 그래프를 구해야 된다.
해당 그래프는 2차 방정식이고, 세 개의 점을 지난다.

\(O=(0,0), A=(2,4),B=(4,0)\) \(y=ax^2+bx+c\)
(0,0) 대입
\[c=0\]
(4,0) 대입
\[b=-4a\]
(2,4) 대입
\[a=-1, b= 4\]

\[y=-x^2+4x\]

12미터 위에서 지상에 착지 했을 때의 거리는 해당 그래프에서 4 - 12 = -8 즉, y = -8 일 때의 x좌표를 구하면 된다

\(-8 = -x^2+4x\)
\(x^2-4x-8=0\)
\(x= 5.46\)

총 이동거리

\[8\times3.732+5.46=35.32 m\]

문제13

원점에서 좌표까지의 거리를 구하는 공식을 쓰면 쉽게 구할 수 있다.

\(O=(0,0,0),A=(2,3,5)\)
\(|\overline{OA}|=\sqrt{(2-0)^2+(3-0)^2+(5-0)^2}\)

정답은 b,e,f

문제14

비율 방정식이다.한 시간은 3600초, 구하고자 하는 초는 x라 했을때 다음과 같이 쓸 수 있다.
\(1440:3600=13:x\)
\(x = \frac{3600\times13}{1440}\)
\(x = 32.5\)

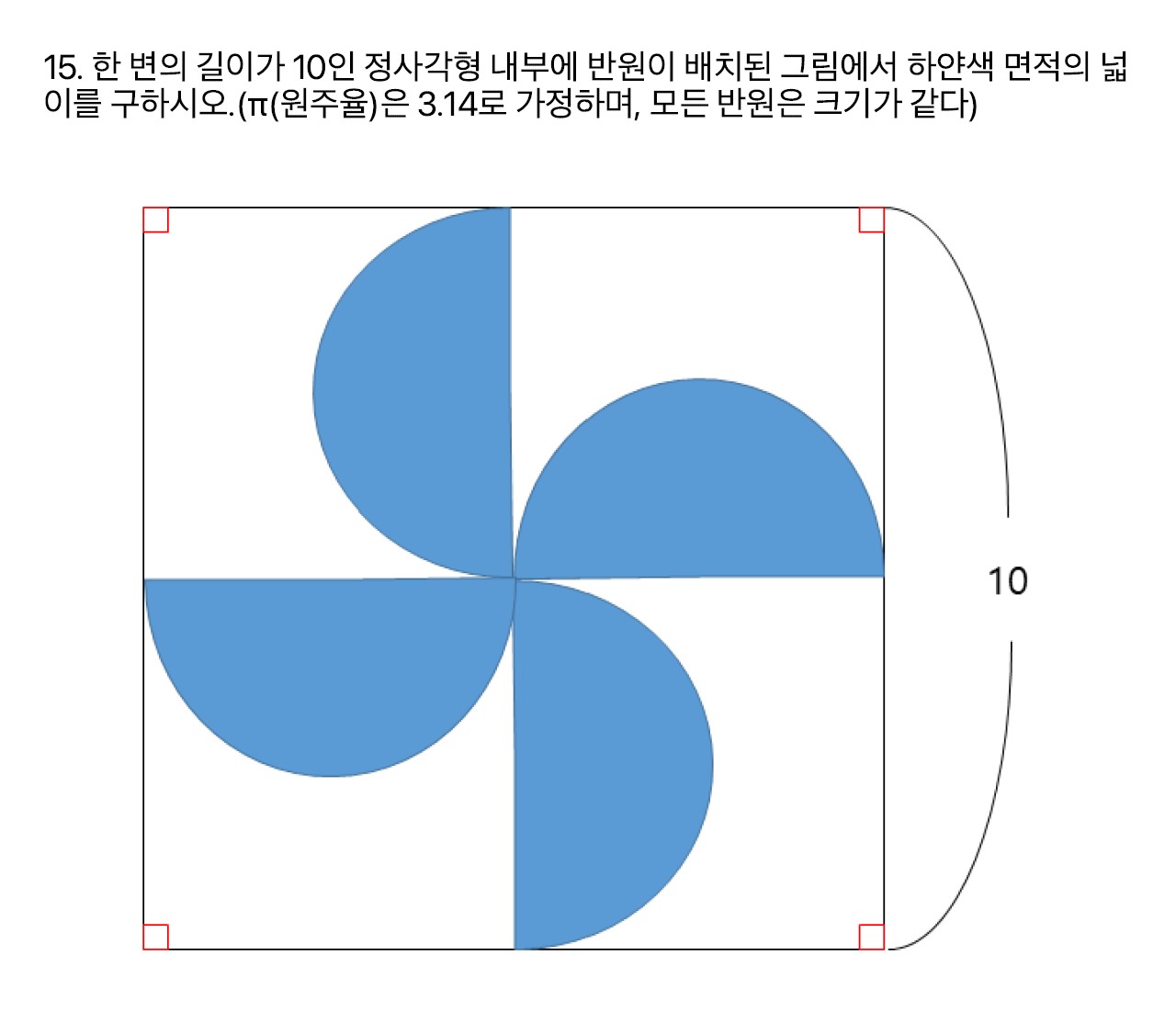
문제15

흰 네모의 면적에서 파란 원 두 개를 뺀 값과 같다.

\[10\times10 - 3.14\times2.5^2\times2 = 60.75\]

문제16

원점에서 각각의 위치까지 이동하는 것을 벡터로 놓는다.

\[\overrightarrow{A}=(5,0,7),\overrightarrow{B}=(12,3,-2)\]

벡터 A 에 벡터 B 를 빼면, 이동한 것에 대한 벡터 C 가 나온다.

\(\overrightarrow{A}-\overrightarrow{B}=\overrightarrow{C}\)
\(\overrightarrow{C} = (5-12,0-3,7-(-2)) = (-7,-3,9)\)

해당 벡터의 크기를 구하면 이동거리가 된다.

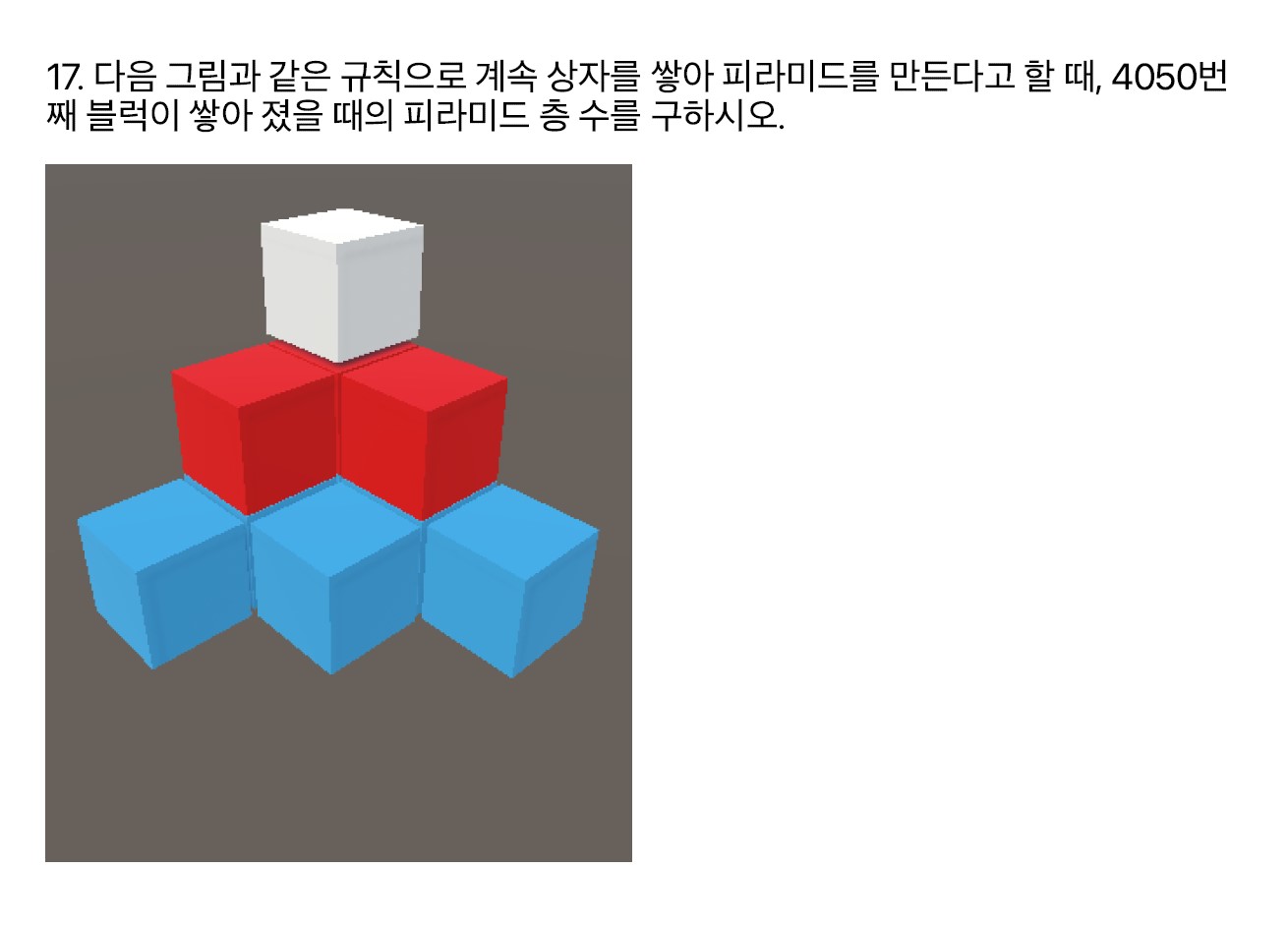
\[|\overrightarrow{C}|=\sqrt{7^2+3^2+9^2} = \sqrt{139}\]

문제17

수열이 제대로 기억이 나지 않았다. 고등학교 공부 부터 다시 해야 될 것 같다.
각 층이 수열의 합 이라는 것 까지는 알고 구했지만
거기서 그 이전층들의 합까지 더해야 하는 이중 합 구조라서 알기 쉽지 않았다
해당 문제는 Chatgpt를 통해 식을 찾았다. 시그마 공식 참조.
각 층의 블럭 갯수를 \(a_n\) 이라고 하자 그러면

\(a_1=1,a_2=1+2,a_3=1+2+3\)
\(,a_4=1+2+3+4\dots\)

\(a_n\) 은 첫 항이 1이고 공차가 1인 등차 수열의 합이다.
\(a_n =\frac{n(2a+(n-1)d)}{2}=\frac{n(n+1)}{2}\)

\(a_n\) 의 합을 \(S_n\) 이라고 하면 다음과 같다
\(S_n = \sum_{k=1}^{n} \frac{K(K-1)}{2}\)
\(=\frac{1}{2}(\sum_{k=1}^{n} K^2 + \sum_{k=1}^{n} K )\)

각 시그마 항의 공식은 다음과 같다.

\(\sum_{k=1}^{n} K^2 = \frac{n(n+1)(2n+1)}{6}\)
\(\sum_{k=1}^{n} K = \frac{n(n+1)}{2}\)

이것들을 더하면 다음과 같이 된다

\(\frac{n(n+1)(2n+1)}{6} + \frac{n(n+1)}{2}\)
\(= n(n+1) \times \frac{(2n+1)+3}{6}\)
\(=\frac{n(n+1)(n+2)}{3}\)

다시 식으로 돌아와서

\[S_n = \frac{1}{2}\frac{n(n+1)(n+2)}{3}=\frac{n(n+1)(n+2)}{6}\]

이제 \(S_n\) 이 4050을 초과 하는 \(n\) 을 찾으면 된다.

\(n = 28\) 일때 4060이다.
그러므로 28층.

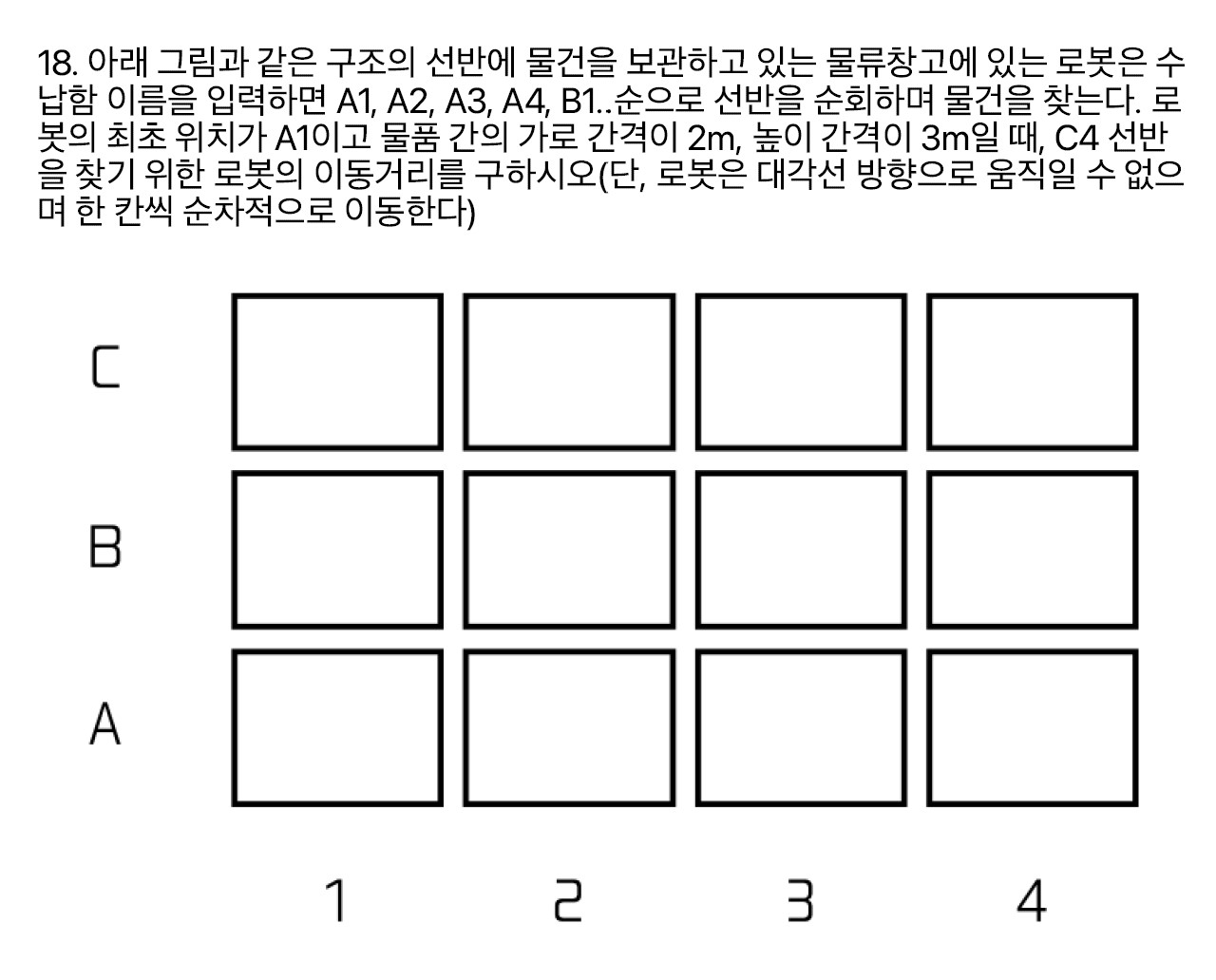
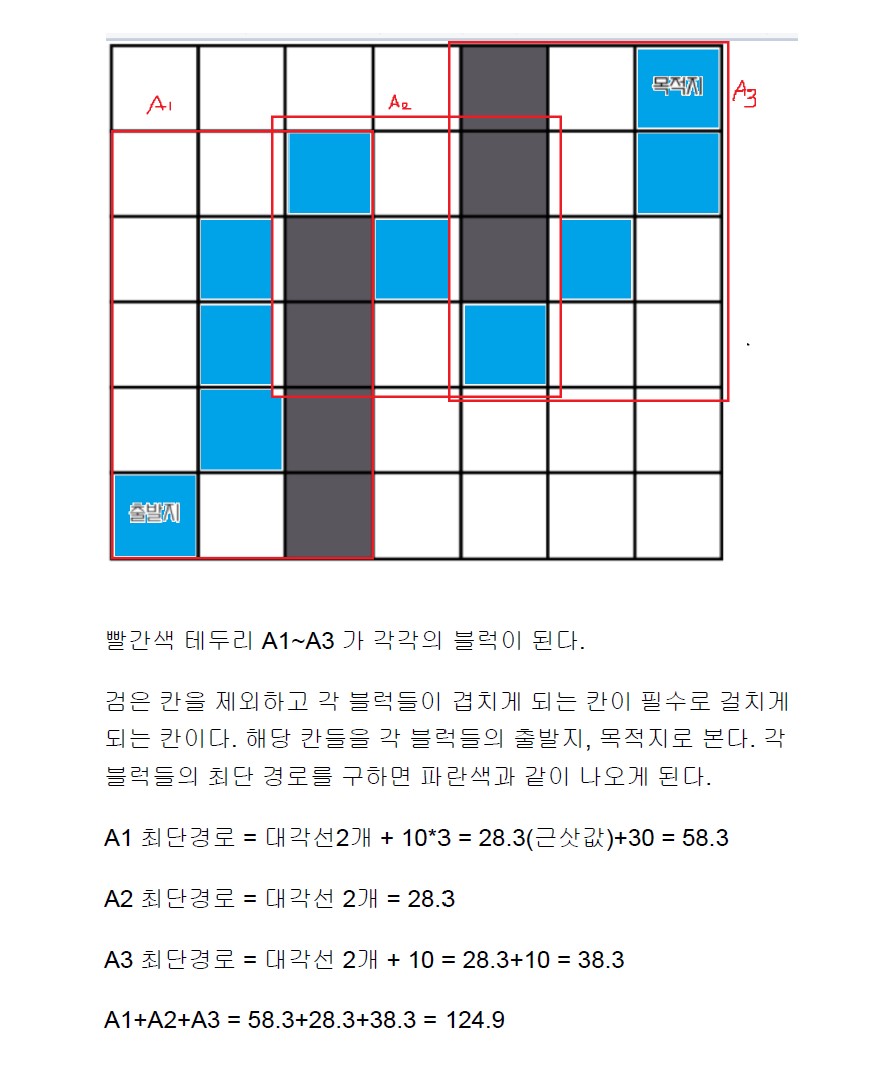
문제18

데이터를 찾는 알고리즘과 관련된 문제다. 거리 = 시간으로 생각하면 된다.
이것이 대규모가 됐을 때, 어떻게 효율적으로 데이터를 찾는 시간을 줄이는 지가 중요하다.

문제19

\(3x=24-4.5\)
\(x=\frac{19.5}{3}=6.5\)

문제20

최소 공배수를 구하는 문제다.
70과 40의 최소 공배수는 280이다.
\(280 = 6\times4+40\)

2150에서 4시간 40분을 더하면 2630
새벽 2시 30분이다.

문제21

분침의 회전 = 7번 회전 + 40분 만큼의 회전
\(360^\circ\times7 + 360^\circ\times\frac{2}{3}=2760^\circ\)
시침의 회전 = 7시간 만큼의 회전 + 40분 만큼의 회전
\(360^\circ\times\frac{7}{12}+360^\circ\times\frac{1}{12}\times\frac{2}{3} = 230^\circ\)

\[2760+230=2990^\circ\]

문제22

최단경로 알고리즘 문제

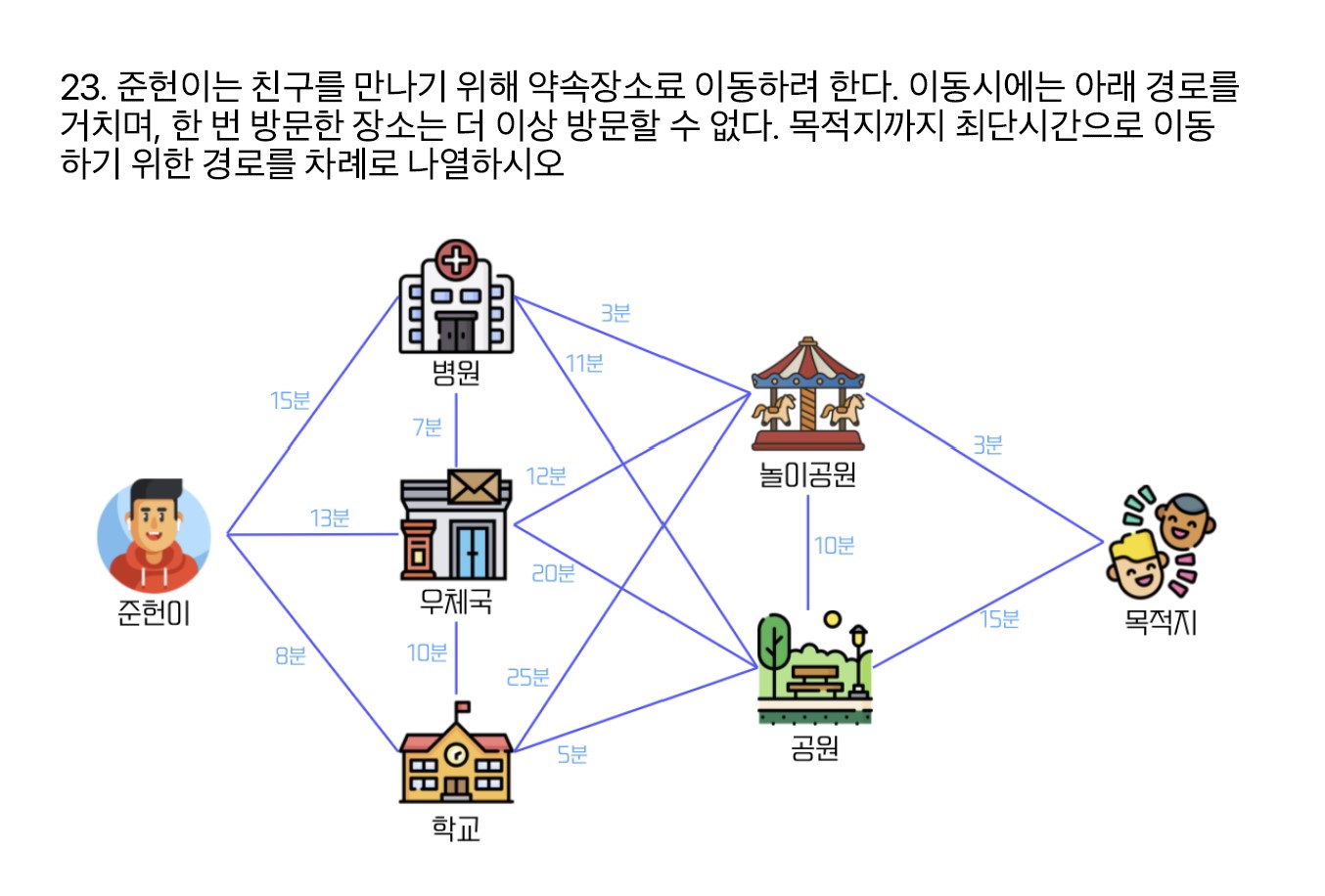
문제23

같은 수강생에게 들은 것인데
다익스트라 알고리즘(Dijkstra Algorithm)과 관련 있을거라 한다

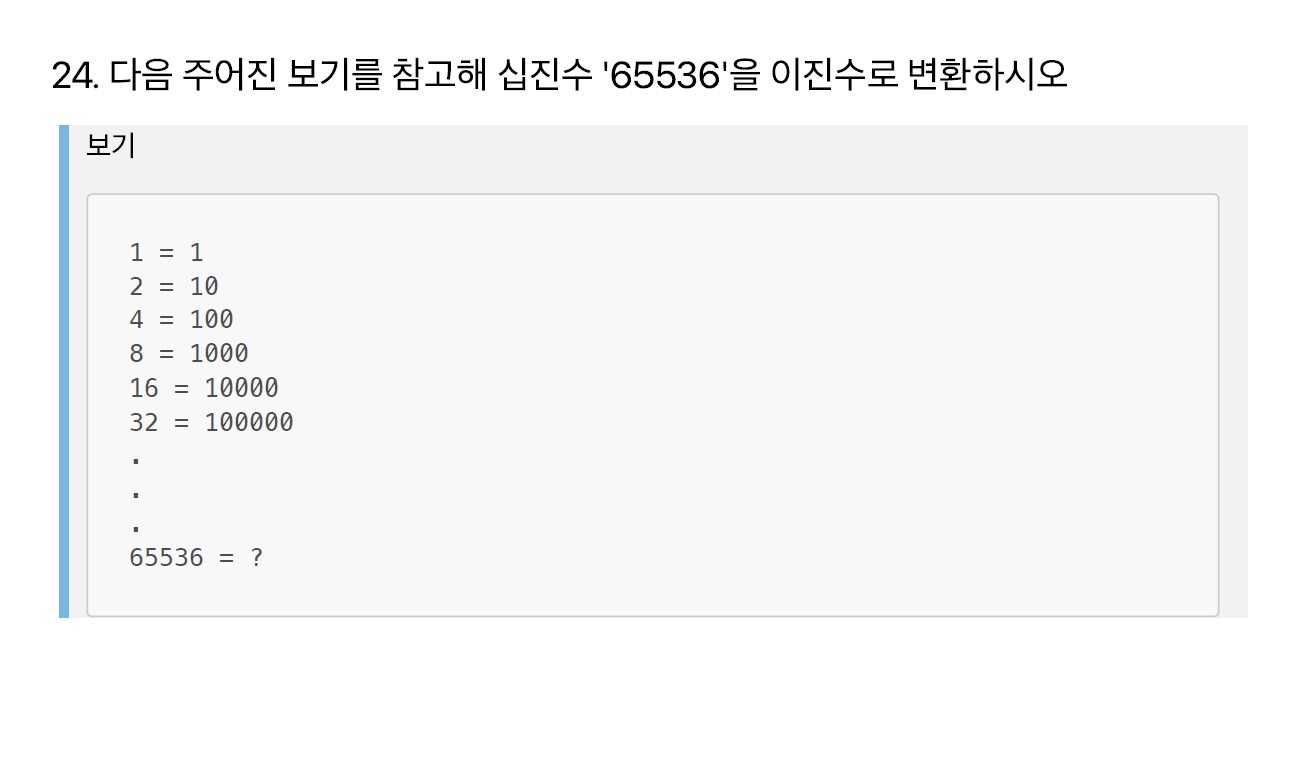
문제24

n진수 변환법을 알면 쉬운 문제다
10진수를 2진수로 변환 하는 방법의 예시는 아래와 같다

\[32 = 2^5\times1+2^4\times0+2^3\times0+2^2\times0+2^1\times0+2^0\times0\]

같은 방법으로 문제의 숫자를 바꾸면 된다

\(2^{16} =65536\)
\(=2^{16}\times1+2^{15}\times0+\dots+2^0\times0=65536\)

그러므로 정답은

\(10000000000000000\dots\) (0이 16개)

문제25

\[\overrightarrow{a}+\overrightarrow{b}=(4+2,1+3) =(6,4)\]

문제26

원점 \(O\) 와 (1,0) 방향으로 미는 힘을벡터 \(\overrightarrow{a}\) 라 했을 때
문제를 다음과 같이 표현할 수 있다.

\[O + 4\overrightarrow{a} = (0+4,0+0) = (4,0)\]

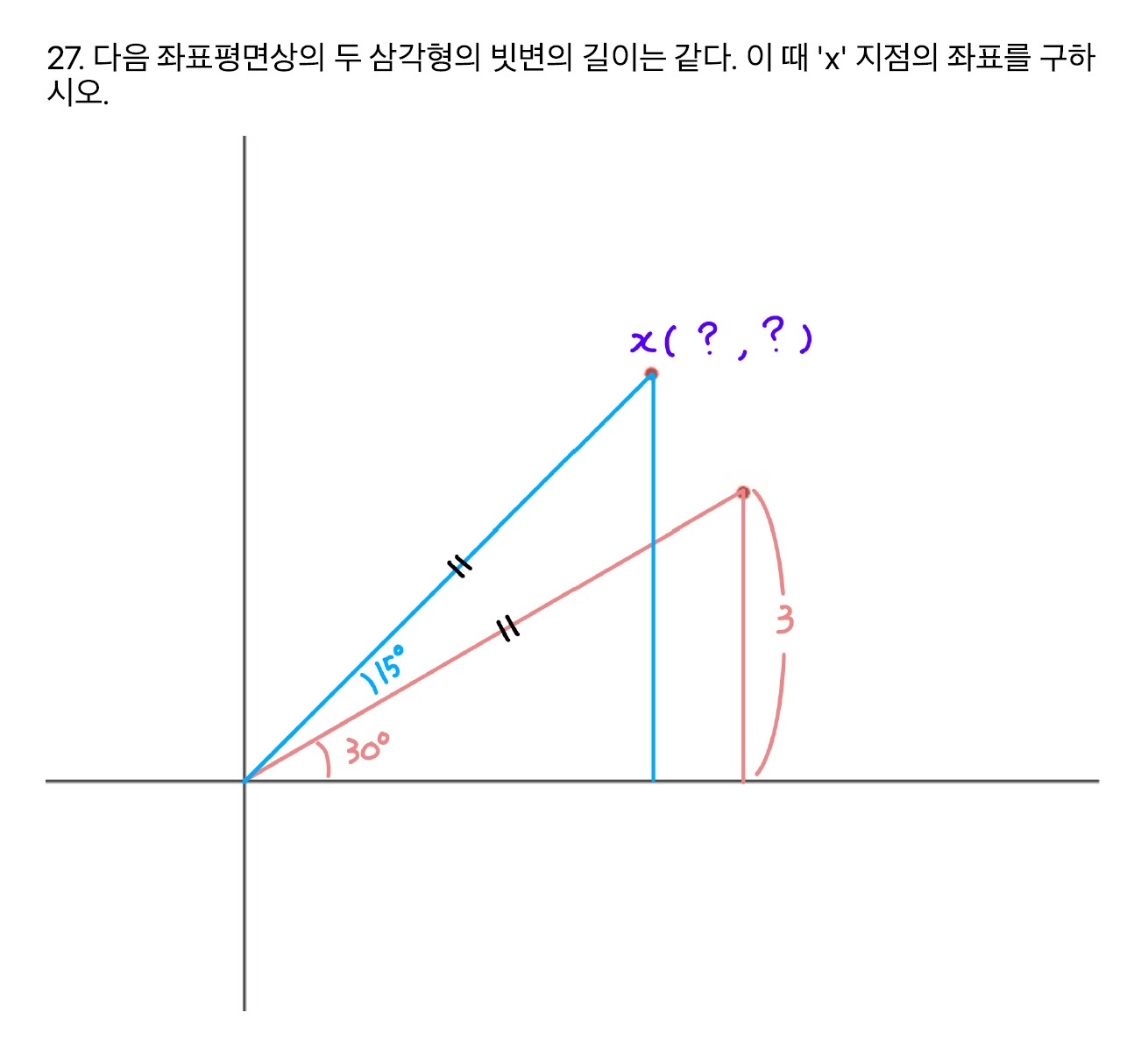
문제27

삼각함수 문제다
파랑 삼각형의 꼭짓점을 \(x(a,b)\) 라고 해보자
그리고 파랑 삼각형과 x축 과의 각을 \(\theta\)라고 하겠다
간단하게 \(\theta = 15^\circ+30^\circ = 45^\circ\) 인 것을 알 수 있다
삼각함수를 통해 분홍 삼각형의 빗변 길이를 알 수 있다
빗변 길이 = \(A\)
\(\sin30^\circ = \frac{1}{2} = \frac{3}{A}\)
\(1 \times A =3 \times 2\)
\(A = 6\)

파랑 삼각형은 이등변 삼각형이고
예각 하나가 \(45^\circ\) 이므로 점 \(x\) 의 \(a,b\) 값은 서로 같다

\(a : 6 = 1 : \sqrt{2}\)
\(a = \frac{6}{\sqrt{2}} = 3\sqrt{2}\)

\[\therefore x=(3\sqrt{2},3\sqrt{2})\]

문제28

백분율 문제다
\(\frac{ \text{사냥한 몬스터} }{ \text{전체 몬스터} }\times 100\)
\(= \frac{378}{1500} \times 100\)

\[= 25.2 \%\]

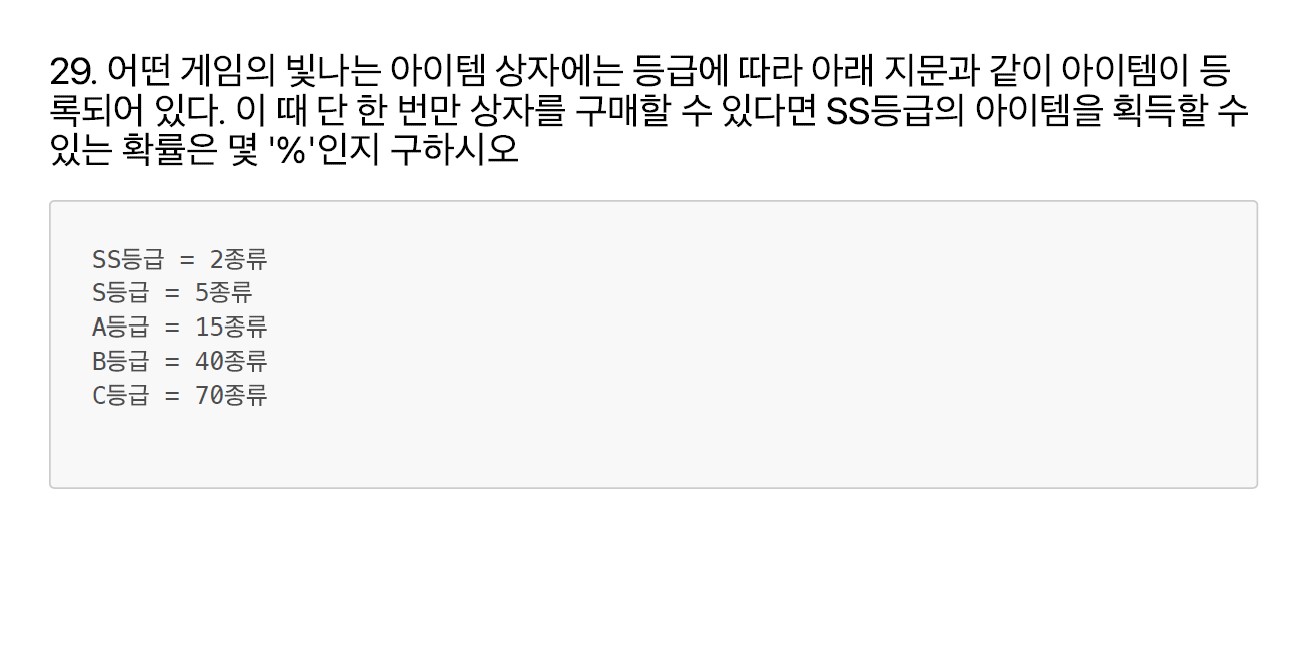
문제29

간단한 확률문제

\(\frac{\text{SS등급}}{\text{전체 합}} = \frac{2}{2+5+15+40+70} = \frac{2}{132}\)
\(\frac{2}{132} \times 100 = 1.51\)

\[\therefore \, 1.5\%\]

문제30

논리 추론 문제인데, 해당 문제는 풀지 못했다

첫 번째 대화에서 재성이가 준헌이는 절대 생일을 모를 것이다!
라는 발언이 첫 번째 논리 포인트다
만약 준헌이가 알고 있는 날이 17일 또는 16일 일 경우, 해당 월은 각각 6월 또는 7월이 되고, 준헌이는 생일을 정확히 맞출 수 있다.
하지만 재성이는 준헌이가 절대 생일을 모를 것이라고 했다
그 말인 즉슨, 재성이가 정택이에게 들은 월이 8월 또는 9월이라는 것이 유추된다
남은 것은 8월 12일, 14일 그리고 9월 12,13,15일 인데
다음 문장을 보도록 하자
준헌이는 처음에는 몰랐지만 이제는 안다고 한다
즉 8월 9월로 특정 되면서 자연스럽게 생일을 알게 되었다는 것이다
준헌이가 알고 있는 날이 12일이면, 준헌이는 생일을 특정할 수 없다. 그러므로 8월 14일, 9월 13일, 15일이 후보가 된다
마지막 문장을 보자
재성이 또한 생일을 알겠다고 한다
만약 13일이나 15일 이면 재성이는 생일을 유추할 수 없다
남은 날은 8월 14일이 된다

그러므로 정답은 8월 14일

마무리

레벨 테스트를 진행하면서 초등~고등 과정까지 광범위하게 리마인드를 해볼 수 있었다
프로그래밍과 연관을 지어 곱씹어 보니 앞으로 어떻게 공부를 할지 방향성도 보이게 됐다
모든 과정이 끝난 후 이 테스트를 돌아보면 느낄 바가 무엇일지 궁금하다

수학, 알고리즘

수학 컴퓨터 언어 알고리즘 기초 사전캠프