게임학원 사전캠프 정리 및 복습 1

유니티 엔진에서 어떤 부분에 수학이 쓰일까?

게임 자체가 거대한 수학이라고 해도 과언이 아닐 것이다. 오늘은 간략하게 게임에서 사용되는 수학은 어떤 것들이 있는지, 간략하게 알아보고자 한다.

---

벡터(Vector)

세기의 정도와 방향의 정보가 있는 값이다.
예시 2차원 벡터
\(\overrightarrow{A} = (5,5)\)

참고

• 유니티에서 백터의 내적과 외적이 갖는 의미
• (유니티)벡터 연산의 이해
• Markdown mathjax
• LaTeX/Mathmatics

---

벡터의 합 (벡터)

물리 부분에서 활용하기 좋음. 움직이는 물체에 플레이어가 충격을 가햇을 때, 물체가 힘을 받은 이후 이동하게 될 방향 계산 가능.

\[\overrightarrow{A} = (5,5) , \overrightarrow{B} = (-10,-2)\] \[\overrightarrow{A} + \overrightarrow{B}\] \[= \overrightarrow{C}(5+(-10), 5+(-2))\] \[\overrightarrow{C} = (-5,3)\]

---

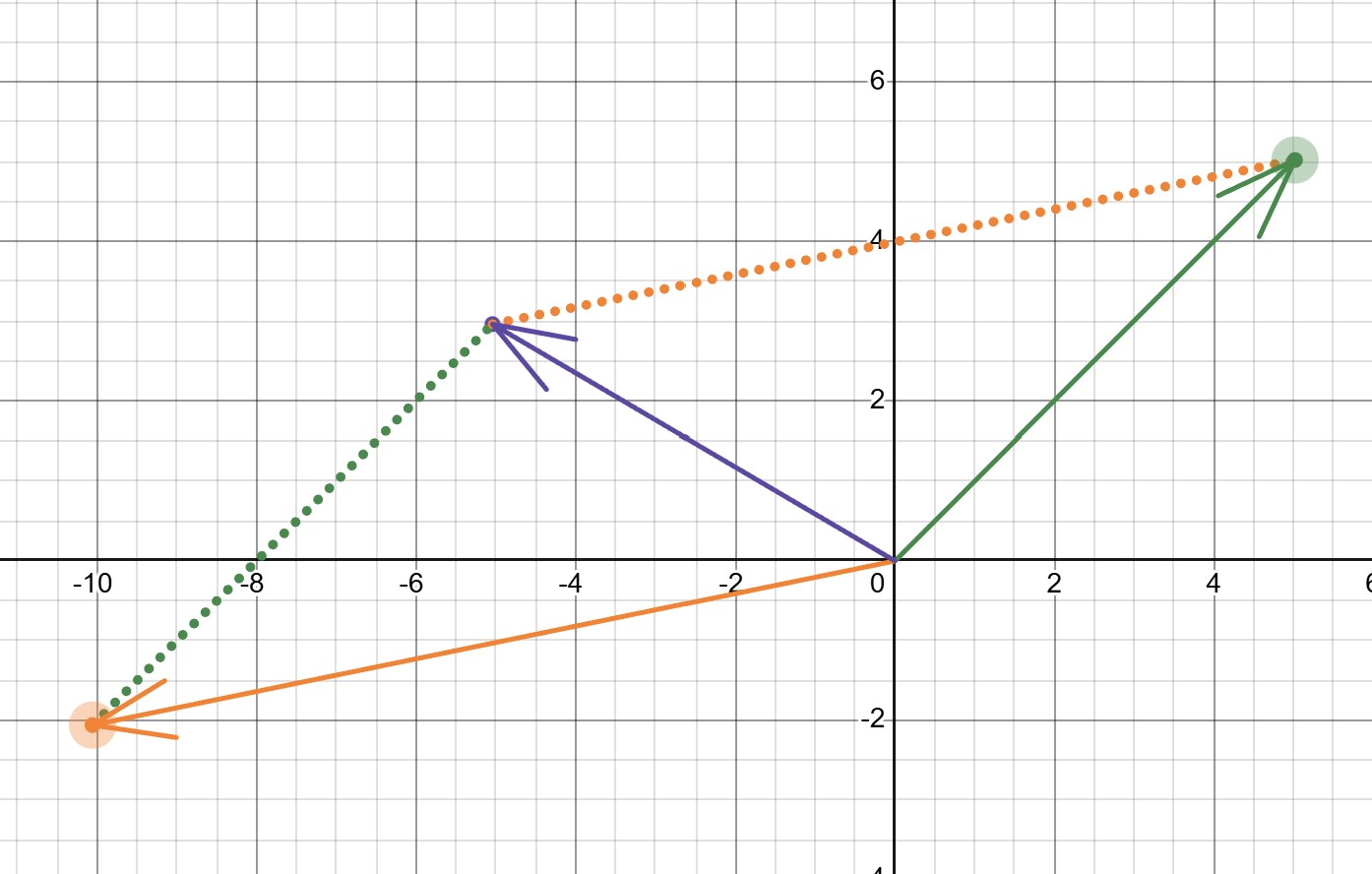
벡터의 내적(Dot Product, 스칼라)

플레이어 기준에서 물체의 앞뒤 판별을 간단하게 가능 - > 시야각 내부에서의 옵젝 존재 여부도 확인 가능

• \[\overrightarrow{A} \cdot \overrightarrow{B}\]

\[= 5 \times (-10) + 5 \times (-2) = -60\]

• \[|A||B| \cos \theta\]

\[= \sqrt{5^2+5^2} \times \sqrt{(-10)^2+(-2)^2}\times \cos\theta\]

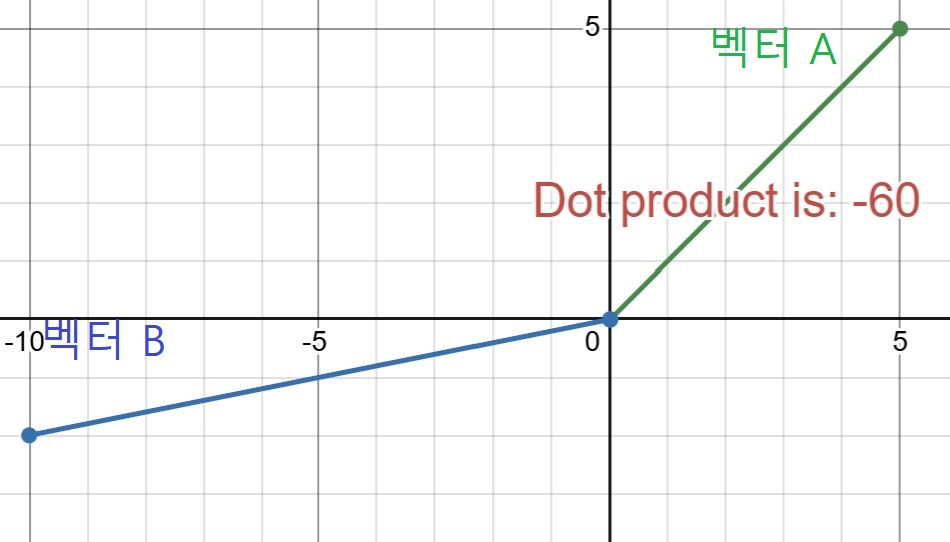
플레이어가 벡터A이고 물체가 벡터B라고 했을 때, 두 벡터의 내적이 음수라면 물체는 플레이어의 뒤에 있다고 판단할 수 있다. \(\overrightarrow{A} \cdot \overrightarrow{B} < 0\)

---

행렬식

2X2 행렬식(Determinant)

\[A= \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad-bc\]

3X3 행렬식

\(B=\begin{vmatrix} x_1 & x_2 &x_3 \\ y_1 & y_2 &y_3 \\ z_1 & z_2 &z_3 \end{vmatrix}\)
\(= x_1\begin{vmatrix} y_2 & y_3 \\ z_2 & z_3 \end{vmatrix} - x_2\begin{vmatrix} y_1 & y_3\\ z_1 & z_3 \end{vmatrix} + x_3\begin{vmatrix} y_1 & y_2\\ z_1 & z_2 \end{vmatrix}\)

---

벡터의 외적(Cross Product, 벡터)

방향을 판단하는 데 사용함. 계산 결과가 계산에 참여한 벡터들과는 수직 벡터로 나오기 때문에, 두 벡터가 만나 면을 이루는 평면을 구하는 데에도 사용됨. 행렬식을 사용한다.
i, j, k는 각각 x, y, z 축의 방향벡터이다.

\[\overrightarrow{A} = (x_a, y_a,z_a), \overrightarrow{B} = (x_b,y_b,z_b)\] \[\overrightarrow{i}=(1,0,0), \overrightarrow{j}=(0,1,0), \overrightarrow{j}=(0,0,1)\]

• 백터의 외적 표시 및 계산법

\(\overrightarrow{A} \times \overrightarrow{B}\) \(=\begin{vmatrix} i & j & k \\ x_a & y_a & z_a \\ x_b & y_b & z_b \end{vmatrix}\)
\(= i\begin{vmatrix} y_a & z_a \\ y_b & z_b \end{vmatrix} - j\begin{vmatrix} x_a & z_a\\ x_b & z_b \end{vmatrix} + k\begin{vmatrix} x_a & y_a\\ x_b & y_b \end{vmatrix}\)

---

두 벡터의 외적의 크기

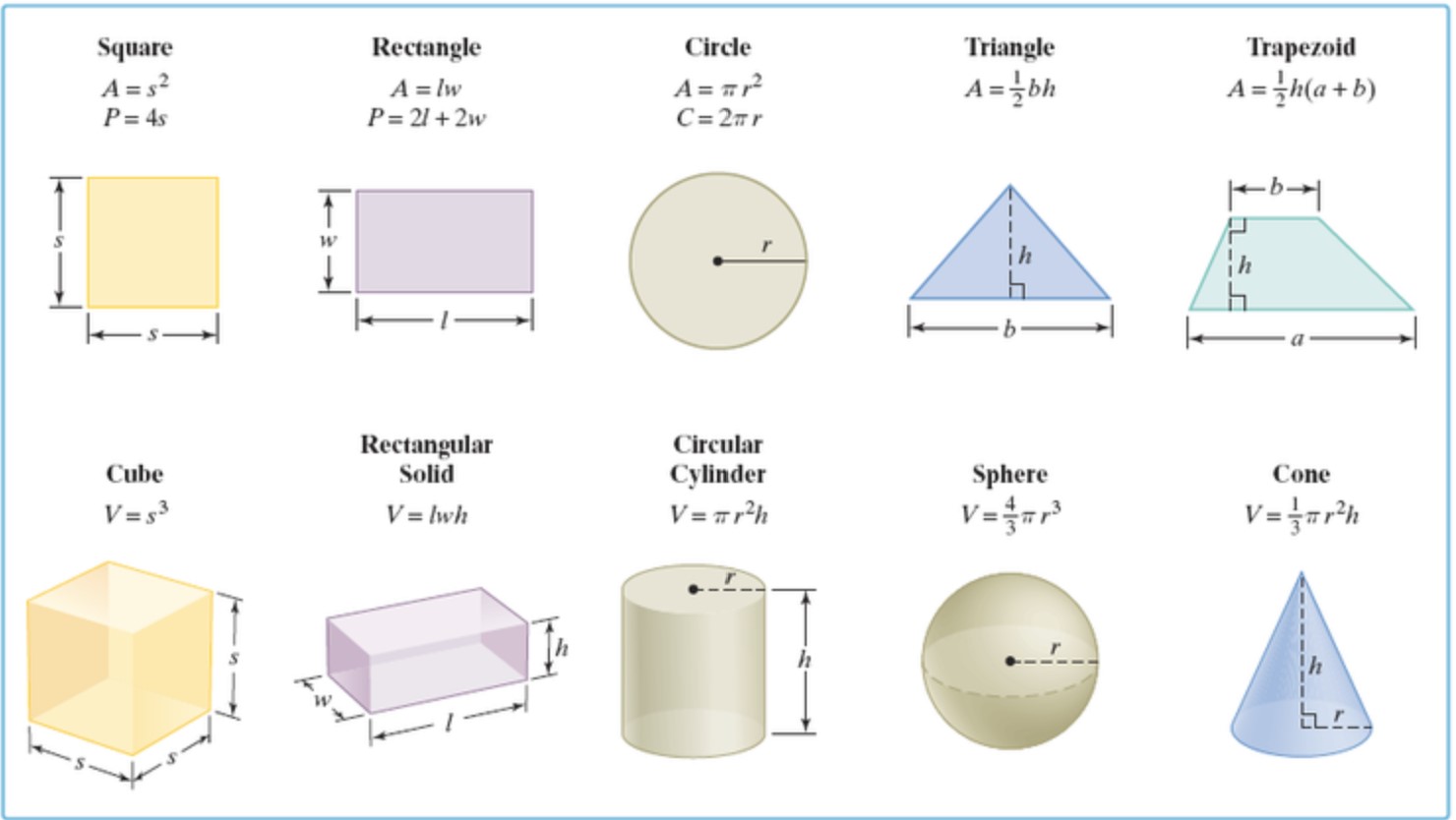
\[| \overrightarrow{A} \times \overrightarrow{B}| = |\overrightarrow{A}| |\overrightarrow{B}| \sin\theta\]

---

물체의 넓이, 부피 공식들

게임에서 은근히 자주 쓰게 될 공식들이다. 모르면 걍 구글링을 하자.

• 검을 휘둘렀을 때, 히트박스의 면적이 얼마나 되는지 알고 싶을때(호의 넓이)
• 플레이어가 화면상에서 차지하는 비율을 알아야 할 때
  \(\frac{플레이어 넓이}{해상도 넓이}\times 100\)
  \(= 플레이어의 화면 차지 백분율\%\)

이후 대학수학, 공학수학을 다시 훑어봐야 할 것 같음